|
Information about locks themselves. Questions, tips and lock diagram information should be posted here.
 by 1more » 8 Mar 2013 12:00 by 1more » 8 Mar 2013 12:00
WOW, thanks for those pictures LockDocWa! I'd be too paranoid that the key would get stuck to use a biting like that but I now believe it can be done successfully. Learn something new everyday 
-
1more
-
- Posts: 18
- Joined: 8 May 2012 11:48
- Location: Chicago
 by minifhncc » 8 Mar 2013 20:13 by minifhncc » 8 Mar 2013 20:13
LockDocWa wrote:Corbin cylindrical / deadbolt or any large format key will use the 14MC.
I don't think so... e.g. COR26S If and when you get an HPC1200, all the info is on the cards.
I have a HPC 1200...
-
minifhncc
-
- Posts: 284
- Joined: 10 Jun 2011 23:03
 by LockDocWa » 8 Mar 2013 21:45 by LockDocWa » 8 Mar 2013 21:45
Post a photo of the COR26S.
Off the top of my head I don't know what that is.
-
LockDocWa
-
- Posts: 251
- Joined: 21 Sep 2012 9:54
- Location: Longview Washington U.S.A
-
 by LockDocWa » 8 Mar 2013 22:04 by LockDocWa » 8 Mar 2013 22:04
This is a CO26, is this close to what you are talking about?? 
-
LockDocWa
-
- Posts: 251
- Joined: 21 Sep 2012 9:54
- Location: Longview Washington U.S.A
-
 by LockDocWa » 9 Mar 2013 11:54 by LockDocWa » 9 Mar 2013 11:54
From what I've seen , the CEA COR26S = Orion and Ilco A1001EH The A1001EH uses the same card as the rest of the 1001 series. CW-14MC SEE CARD #13 Can we put this to rest now? 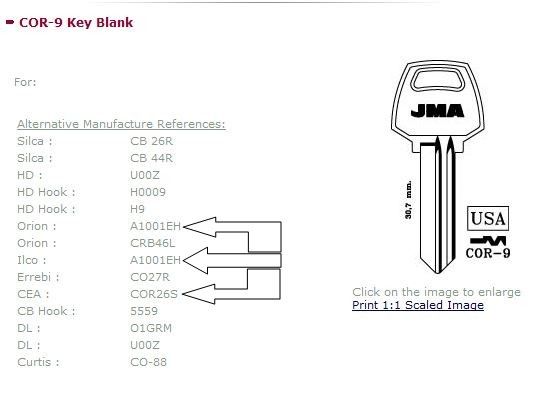 
-
LockDocWa
-
- Posts: 251
- Joined: 21 Sep 2012 9:54
- Location: Longview Washington U.S.A
-
 by Sinifar » 22 Mar 2013 8:53 by Sinifar » 22 Mar 2013 8:53
A MACS "stretcher" - There are times when you do want to do this, but not too often. One of the problems is it won't duplicate with a 45 degree cutter worth a darn.
This maybe an advantage, then it maybe a liability. If you are going to violate the MACS, cut ONLY the cuts required with the steeper angled cutter, and use a standard one for the rest.
Our Framon has "FC 7863" cutter which is a Sargent 76 degree unit. It has a bit wider pin land, and steeper ramps, which can make the thing pull out harder.
Mostly try to stay away from "circus tricks" like this and don't do "cute" things like this without a very good reason. MAKE BIG NOTES in your customer's files when you do, highlight any keys cut with this method, or you will be having fits trying to make more if you don't remember what you did to make the thing work right in the first place.
Sinifar
The early bird may get the worm, but it is the second mouse which gets the cheese!
The only easy day was yesterday.
Celebrating my 50th year in the trade!
-
Sinifar
-
- Posts: 352
- Joined: 24 Feb 2013 11:23
- Location: Securing the Kettle Moraine since 1972
 by PinPopper1 » 26 Mar 2013 8:13 by PinPopper1 » 26 Mar 2013 8:13
Can someone briefly explain MACS for newb's. I am assuming this refers to the maximum allowable difference between cuts in your keys but I am unfamiliar with the rules surrounding this. Also could someone explain how the different cutting wheels affect different keys? It would be greatly appreciated.
-
PinPopper1
-
- Posts: 16
- Joined: 10 Mar 2013 16:58
 by geekmug » 19 Jan 2014 18:01 by geekmug » 19 Jan 2014 18:01
I hate to bring a thread back up from the dead, but I stumbled on this thread when trying to learn how many combinations of keys there are for my house key. This is actually a really hard combinatorics problem because of the MAC, so I was hoping someone had done the math already. I think you would have to break the problem down into different special-cases doing inclusion/exclusion.. or, you can exploit the fact that it's a really small combinatoric space and just brute-force it with a simple Python script: - Code: Select all
DEPTHS = 10
MAC = 7
PINS = 6
def is_valid_mac(key):
for i in range(PINS - 1):
if abs(key[i] - key[i + 1]) > MAC:
return False
return True
def main():
valid = 0
key = [0] * PINS
is_not_done = True
while is_not_done:
if is_valid_mac(key):
valid += 1
for i in range(PINS):
key[i] += 1
if key[i] >= DEPTHS:
key[i] = 0
if i == PINS - 1 :
is_not_done = False
continue
else:
break
print("Valid: %d" % (valid,))
if __name__ == '__main__':
main()
The answer for a 6 pin, 10 depth, 7 MAC key is 753,754. The answer for a 5 pin, 10 depth, 7 MAC key is 79,666. Hope this helps anyone else who stumbles across this thread when searching for this answer.
-
geekmug
-
- Posts: 2
- Joined: 19 Jan 2014 17:47
 by 1more » 20 Jan 2014 9:09 by 1more » 20 Jan 2014 9:09
Holy Cow geekmug that is awesome!!! Thank you for sharing, that was kind of what I was looking for when I started this thread.
-
1more
-
- Posts: 18
- Joined: 8 May 2012 11:48
- Location: Chicago
 by Achyfellow » 20 Jan 2014 9:20 by Achyfellow » 20 Jan 2014 9:20
geekmug wrote:I hate to bring a thread back up from the dead, but I stumbled on this thread when trying to learn how many combinations of keys there are for my house key. This is actually a really hard combinatorics problem because of the MAC, so I was hoping someone had done the math already. I think you would have to break the problem down into different special-cases doing inclusion/exclusion.. or, you can exploit the fact that it's a really small combinatoric space and just brute-force it with a simple Python script: - Code: Select all
DEPTHS = 10
MAC = 7
PINS = 6
def is_valid_mac(key):
for i in range(PINS - 1):
if abs(key[i] - key[i + 1]) > MAC:
return False
return True
def main():
valid = 0
key = [0] * PINS
is_not_done = True
while is_not_done:
if is_valid_mac(key):
valid += 1
for i in range(PINS):
key[i] += 1
if key[i] >= DEPTHS:
key[i] = 0
if i == PINS - 1 :
is_not_done = False
continue
else:
break
print("Valid: %d" % (valid,))
if __name__ == '__main__':
main()
The answer for a 6 pin, 10 depth, 7 MAC key is 753,754. The answer for a 5 pin, 10 depth, 7 MAC key is 79,666. Hope this helps anyone else who stumbles across this thread when searching for this answer.
I started working on the script when I saw the thread yesterday without checking the last message ahahahaha Very nice
-
Achyfellow
-
- Posts: 131
- Joined: 1 Oct 2013 6:50
 by Evan » 20 Jan 2014 12:41 by Evan » 20 Jan 2014 12:41
geekmug wrote:I hate to bring a thread back up from the dead, but I stumbled on this thread when trying to learn how many combinations of keys there are for my house key.
This is actually a really hard combinatorics problem because of the MAC, so I was hoping someone had done the math already. I think you would have to break the problem down into different special-cases doing inclusion/exclusion.. or, you can exploit the fact that it's a really small combinatoric space and just brute-force it with a simple Python script:
The answer for a 6 pin, 10 depth, 7 MAC key is 753,754.
The answer for a 5 pin, 10 depth, 7 MAC key is 79,666.
Hope this helps anyone else who stumbles across this thread when searching for this answer.
Interesting answer, however that would only define the valid keyspace removing the MACS violations from the original million possible permutations... The number you supplied would have failed to remove undesirable combinations (such as ones with several duplicate bittings adjacent i.e. 444444, OR deal with the key bittings which do not comply with the double step bitting requirement of generating a proper Schlage keying system)... What is possible and what is functionally useable are two entirely separate issues... The real number would require a lot more parameters to be defined... ~~ Evan
-
Evan
-
- Posts: 1490
- Joined: 5 Apr 2010 17:09
- Location: Rhode Island
 by geekmug » 20 Jan 2014 15:21 by geekmug » 20 Jan 2014 15:21
Evan wrote:Interesting answer, however that would only define the valid keyspace removing the MACS violations from the original million possible permutations... The number you supplied would have failed to remove undesirable combinations (such as ones with several duplicate bittings adjacent i.e. 444444, OR deal with the key bittings which do not comply with the double step bitting requirement of generating a proper Schlage keying system)...
What is possible and what is functionally useable are two entirely separate issues...
The real number would require a lot more parameters to be defined...
~~ Evan
Excellent reply. I hadn't even thought of that issue. The double step biting is an interesting rule to impose by Schlage; I am a novice in this area so I don't fully understand why single steps would be a problem, but I assume it's a manufacturing tolerance issue. However, adding in just that rule greatly reduces the keyspace (5-pin: 33,724 and 6-pin: 257,174). The "straight" key (e.g., 444444) is an interesting example of an undesirable key, because it's not really invalid for any obvious reason (however, subtract 10 from both of the counts above if you want to disregard them). I suppose the best argument against such a key is that if someone saw your key, they could easily decode it on sight. I googled arguments to avoid runs and stair-cases, but then I have keys from the manufacturer that fail those criteria. If you add too many additional rules to the key system, then you may reduce the keyspace too much to be useful. For instance, if you disallow any neighboring pins to be the same depth cut, you get 5-pin: 19,222 and 6-pin: 127,344. Incidentally, for a 6-pin key, that rule eliminates stair-case keys. However, for 5-pin, you can still make 12 different stair-case keys (so subtract 12 for 19,210). So the lowest count for what seem like "valid" keys to me is: 5-pin: 19,210 6-pin: 127,344 , which is still a quite healthy number for both. I know that if you need to involve master keying, then you will significantly impact the number of combinations, but that's outside the scope of the question I was asked ("how likely is it that you can walk up to someone's house and put your key in the door and open it?").
-
geekmug
-
- Posts: 2
- Joined: 19 Jan 2014 17:47
 by Evan » 20 Jan 2014 17:06 by Evan » 20 Jan 2014 17:06
geekmug wrote:Excellent reply. I hadn't even thought of that issue. The double step biting is an interesting rule to impose by Schlage; I am a novice in this area so I don't fully understand why single steps would be a problem, but I assume it's a manufacturing tolerance issue. However, adding in just that rule greatly reduces the keyspace (5-pin: 33,724 and 6-pin: 257,174). The "straight" key (e.g., 444444) is an interesting example of an undesirable key, because it's not really invalid for any obvious reason (however, subtract 10 from both of the counts above if you want to disregard them). I suppose the best argument against such a key is that if someone saw your key, they could easily decode it on sight. I googled arguments to avoid runs and stair-cases, but then I have keys from the manufacturer that fail those criteria.
If you add too many additional rules to the key system, then you may reduce the keyspace too much to be useful. For instance, if you disallow any neighboring pins to be the same depth cut, you get 5-pin: 19,222 and 6-pin: 127,344. Incidentally, for a 6-pin key, that rule eliminates stair-case keys. However, for 5-pin, you can still make 12 different stair-case keys (so subtract 12 for 19,210).
So the lowest count for what seem like "valid" keys to me is:
5-pin: 19,210
6-pin: 127,344
, which is still a quite healthy number for both.
I know that if you need to involve master keying, then you will significantly impact the number of combinations, but that's outside the scope of the question I was asked ("how likely is it that you can walk up to someone's house and put your key in the door and open it?").
The double-step bitting requirement of generating a keying system is because of the manufacturing tolerances... The bitting steps are .015" different from each other so that if you had two keys that were identical in each cut except one depth in one position you would experience unintended key interchange... That is a big technical jargon word which says the "different" keys would work in both locks experiencing only a bit of binding on a brand new lock, let alone one that has been used... "Straight" keys (or even keys with only a couple identical bittings adjacent) would leave the locks vulnerable to being easily combed/raked open with very little skill or technique required at all... A "Staircase" key or in the technical term a "declining step key" is undesirable because when the lock and key become worn, the key can be removed before the key pull position and leave the lock in an unsecured state... It has to be a totally declining key for this to apply, with the shallowest cuts at the bow and the deepest cuts at the tip with no rises between, i.e. 123456... But this discussion is the reason why there are rules regarding creating keying systems... The "real" number of different keys which can exist in a 6-pin Schlage lock is 4,096 multiplied by the number of keyways available and then multiplied by the number of different bitting parities possible (pattern of Odd and Even cuts on the key)... In order to say you would not be able to possibly take a random key and use it in an unintended lock you would have to follow all of the same rules you would if you were generating a master key system, so the "real" numbers are much smaller than most people would believe given that 10 depths and 6 pins starts at 1,000,000 possible combinations... ~~ Evan
-
Evan
-
- Posts: 1490
- Joined: 5 Apr 2010 17:09
- Location: Rhode Island
 by somenewguy » 26 Feb 2014 21:37 by somenewguy » 26 Feb 2014 21:37
Just to add my non-math 2 cents; I believe the term used here is 'differs' as in "how many key differs are there in a x pin y cuts z MACS system?"
-
somenewguy
-
- Posts: 214
- Joined: 7 Sep 2013 15:19
Return to Locks
Who is online
Users browsing this forum: Google [Bot] and 5 guests
|
